
| Go back to Sun Hill Observatory |
SHON - Article
Date of publication: 12th October, 2007
Period and Light Curve Analysis of the Eclipsing Binary IL Monocerotis
Petr Molik
Okruzni 103/III, 392 01 Sobeslav, Czech Republic; e-mail: Petr.Molik@vupp.cz
Abstract: In this paper a long-term continuous period increase in the Algol-type eclipsing binary IL Mon is reported for the first time. Analysis of its light curve suggests that if the primary component has spectral type A0V the secondary should be either a subgiant of spectral type G8IV-K4IV or a giant about G3III.
IL Mon (= OV22 = GSC 4837.2525, R.A.(J2000) 7 h 55 m 35.95 s, Decl. (J2000) -03° 34' 55.5", Max. = 10.7 mag V, Min. = 11.6 mag V, Sp. A0 + G-K) is an Algol-type eclipsing binary star. Its variability was discovered photographically by B. S. Whitney at the Observatory of University of Oklahoma in the year 1948. An extended series of photographic plates obtained at this observatory within the years 1947-1950 enabled Whitney (1951) to determine six times of minimum light and calculate preliminary light elements of this variable star:
| Min.I = JD(hel) 24 32 232.772 + 16.1076 x E. |
Whitney considered the possibility that the period was only four days but after re-estimation of the plates he concluded that the period of 16 days should be retained. These light elements were taken into GCVS2 (1958) and GCVS3 (1969-1971).
Quarter of a century later Ahnert (1976) examinated Sonneberg patrol plates from the interval 1950-1975 and found 20 times of minimum light spanning the years 1953-1973 (in fact, 14 of them were instants when the star was near minimum and 6 were times when the star was only fainter than usual). Ahnert revealed the true period which is one fourth of the earlier published value and by combining his and Whitney's minima timings derived the following elements:
| Min.I = JD(hel) 24 32 232.825 + 4.02631 x E |
These light elements were included into GCVS4 (1985-1987). Then until the mid of the 1990s the star had been completely neglected.
I observed IL Mon visually in 1994 and 1995 with the 0.2 m refractor and 0.35 m Maksutov-Cassegrain telescope at the Petøín Hill Observatory in Prague (Czech Republic). Visual estimates were done by the method of Nijland-Blazhko using the B.R.N.O. finding chart. Total 108 estimates were obtained (for details see the page placed here). From 19 estimates obtained on the nights of 1/2 November and 21/22 November, 1994, one normal minimum timing was derived: JDhel 2449678.718. Another time of minimum was determined from 38 estimates done on the night of 6/7 March, 1995: JDhel 49783.402.
Since that time only one CCD minimum timing based on ASAS-3 data (Dvorak, 2004) and one visual minimum timing by R. Meyer (Hübscher et al., 2005) have been published for IL Mon. Kreiner (2004) in his Up-to-date Linear Elements of Eclipsing Binaries gives for this binary the elements:
| Min.I = JD(hel) 24 52 501.15 + 4.026274 x E |
These elements were computed from 13 photographic plate minima of Ahnert and one Meyer's visual minimum timing. The author claims that they are valid for the interval 1955-2004. The period is by 3 second shorter than that published by Ahnert.
The photometric data from sky survey projects ROTSE (Wozniak et al., 2004) and ASAS-3 (Pojmanski, 2003) made public via the Internet enabled me to determine four new minimum timings of IL Mon. They all are normal minima, each obtained by superposition of measurements spread over one or more observing seasons. The period of 4.026328 day was used for superposition of the data. These four new times of minima together with all the above mentioned minimum timings taken from the literature are presented in Table 1.
Table 1. Times of minima for IL Mon.
No. Min.JD(hel) Epoch (O-C) W Meth Observer Source
1 32232.768 0 -0.057 1 S B.S.Whitney AJ 55:230
2 32232.772 0 -0.053 1 S B.S.Whitney AJ 55:230
3 32232.825 0 0.000 1 P P.Ahnert IBVS 1150
4 32643.514 102 0.005 1 S B.S.Whitney AJ 55:230
5 32667.685 108 0.019 1 S B.S.Whitney AJ 55:230
6 32675.720 110 0.001 1 S B.S.Whitney AJ 55:230
7 32965.65 182 0.037 1 S B.S.Whitney AJ 55:230
8 33416.684 294 0.124 1 S B.S.Whitney AJ 55:230
9 34451.39 551 0.068 1 P P.Ahnert MVS 7(7):171
10 34455.45 552 0.102 1 P P.Ahnert MVS 7(7):171
11 34471.34 556 -0.113 1 P P.Ahnert MVS 7(7):171
12 35216.37 741 0.049 1 P P.Ahnert MVS 7(7):171
13 35514.39 815 0.122 1 P P.Ahnert MVS 7(7):171
14 35542.39 822 -0.062 1 P P.Ahnert MVS 7(7):171
15 36605.44 1086 0.042 1 P P.Ahnert MVS 7(7):171
16 36613.42 1088 -0.030 1 P P.Ahnert MVS 7(7):171
17 37366.37 1275 -0.000 1 P P.Ahnert MVS 7(7):171
18 37579.63 1328 -0.135 1 P P.Ahnert MVS 7(7):171
19 38441.43 1542 0.035 1 P P.Ahnert MVS 7(7):171
20 39194.35 1729 0.035 1 P P.Ahnert MVS 7(7):171
21 39391.62 1778 0.016 1 P P.Ahnert MVS 7(7):171
22 39528.40 1812 -0.099 1 P P.Ahnert MVS 7(7):171
23 39528.46 1812 -0.039 1 P P.Ahnert MVS 7(7):171
24 39967.37 1921 0.003 1 P P.Ahnert MVS 7(7):171
25 40148.57 1966 0.020 1 P P.Ahnert MVS 7(7):171
26 40917.54 2157 -0.036 1 P P.Ahnert MVS 7(7):171
27 41356.40 2266 -0.043 1 P P.Ahnert MVS 7(7):171
28 41988.55 2423 -0.024 1 P P.Ahnert MVS 7(7):171
29 49678.718 4333 -0.108 10 V P.Molik OEJV 60
30 49783.402 4359 -0.108 10 V P.Molik OEJV 60
31 51550.9597 4798 -0.1007 20 C - this paper
32 52698.4660 5083 -0.0927 20 C - this paper
33 52718.5944 5088 -0.0959 20 C - this paper
34 53044.71 5169 -0.111 0 C - IBVS 5542
35 53076.92 5177 -0.112 0 V R.Meyer BAVM 174
36 53797.6646 5356 -0.0768 20 C - this paper
Notes to the table:
Times of minima are given in the format JD(hel) - 2400000.
Epochs and O-C residuals were calculated with respect to the elements:
Min.I = JD(hel) 2432232.825 + 4.02631 x E. The O-C values are given
in fractions of a day.
W = weight.
Method of observation: V = visual, P = photographic patrol plate,
S = series of photographs, C = CCD camera.
Remarks on individual minima:
No. 1: 4 observations on the ascending branch of the minimum
No. 2: initial epoch from elements
No. 3: initial epoch from elements
No. 4: 1 observation on the ascending branch of the minimum
No. 5: 5 observations on the descending branch of the minimum
No. 6: 2 observations on the descending branch of the minimum
No. 7: low accuracy, 6 observations in the total phase of the minimum
No. 8: 2 observations on the ascending branch of the minimum
No.31: time of minimum determined by P. Molik from the ROTSE data, without
filter, superposition of measurements from the interval
JD 51486-51632
No.32: time of minimum determined by P. Molik from the ASAS-3 data,
filter V, superposition of measurements from the interval
JD 51921-53053
No.33: time of minimum determined by P. Molik from the ASAS-3 data,
filter V, superposition of measurements from the interval
JD 52190-53069
No.34: time of minimum determined by S. W. Dvorak from the ASAS-3 data,
filter V
No.35: superposition
No.36: time of minimum determined by P. Molik from the ASAS-3 data,
filter V, superposition of measurements from the interval
JD 53753-53895
|

An O-C diagram of IL Mon based on the light elements given by Ahnert (1976) is displayed in Figure 1. It shows that the visual and CCD minima at the right side of the diagram strongly deviate from the ephemeris. Moreover, the O-C residuals from the last 11 years clearly demonstrate that orbital period of IL Mon continuously increases. The old photographic minima have large scatter of O-C values but they do not contradict the continuous period change. Therefore I attempted to fit a parabola to all the minimum timings, giving different weights to photographic (w=1), visual (w=10), and CCD observations (w=20). The two minimum times published by Dvorak (2004) and Hübscher et al. (2005) seem to be incorrect and were excluded from the parabola fitting (w=0). The result is given here with mean errors in parentheses (in Figure 1 it is represented by the continuous curve):
| Min.I = JD(hel) 24 43 103.764(±0.012) + 4.0262850(±0.0000062) x E + 1.17(±0.07) x 10^-8 x E^2 |
These quadratic elements describe the course of O-C residuals much better than any of the above mentioned linear elements. As to the cause of the continuous period increase there are two possible explanations: mass transfer between the components of the binary and the presence of a third body in the system. Despite the fact that many Algol-type eclipsing binaries have semi-detached configuration a long term continuous period change due to mass transfer would be quite unusual in such a system. As far as we know, intrinsic period changes in Algols are discontinuous, most often abrupt. In the case of the presence of a third body the parabola would be part of a sinusoid with a period longer than 120 years and full amplitude larger than 0.2 day. Because the distance to IL Mon is large (Dworak, 1975, gives for its photometric parallax the value of 0.0012 arcsec) the hypothetical third body could be directly detectable only spectroscopically.
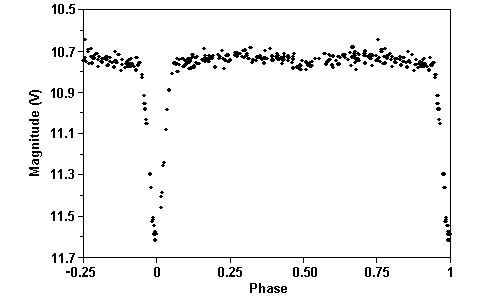
Figure 2, containing a sample of ASAS-3 measurements obtained in filter V, shows that the light curve of IL Mon is as of typical Algol: sharp primary minimum is 0.9 mag deep (1.0 mag pg according to Ahnert, 1976) while the very shallow secondary is only about 0.02 mag deep. Brightness outside eclipses slightly changes due to small ellipticity of the component stars. More precise processing of the ASAS-3 data gives the following values for the light curve extrema: Min.I = 11.59 mag V, Min.II = 10.78 mag V, Max.I = Max.II = 10.72 mag V, the brightness outside eclipses changes between 10.72 and 10.76 mag V. The secondary minimum occurs exactly at phase 0.5 and its duration is equal to the primary which indicates a circular orbit.
It is interesting to note, that according to Whitney (1951) the primary eclipse lasts 7.2 hours, according to Ahnert (1976) it lasts 6.5 hours, but the duration of primary eclipse determined by me from ASAS-3 data is 11.6 hours. Whitney (1951) as well as Ahnert (1976) found constant light in primary minimum lasting 3.1 hours and 2.9 hours, respectivelly. In my visual observations, in ROTSE data, and in ASAS-3 data there are no signs of phase of constant light at the bottom of primary eclipse. These differences seem to be larger than observational errors and may suggest secular variability of the light curve. Only further more precise measurements can prove or disprove this suggestion.
First attempt on determination of geometric and physical parameters of IL Mon was done by Herczeg and Kerrigan (1974). They used the photographic light curve of Whitney (unpublished), his incorrect 16-day period and the spectral type A0 published for this star by Götz and Wenzel (1961). The result was that IL Mon is a detached binary system composed of similar components (both spectral type A), one of them evolved slightly above the main sequence.
Svechnikov et al. (1980) classified IL Mon as detached system composed of two main sequence stars. GCVS4 (1985) presents the system as semi-detached with a mark notifying that this classification is uncertain.
According to Svechnikov and Kuznetsova (1990) the binary contains two main sequence stars in detached configuration. Relative radii of the primary and the secondary components are 0.157 and 0.066, respectively. Radii of the two components and the distance between their centers in units of solar radius are 2.50, 1.05 and 16.00, respectively. Mass ratio of the components (q = M2/M1) is 0.400. Spectral types of the components are A0 (primary) and G9 (secondary). It is evident that the authors based their analysis on Ahnert's photographic light curve. However, it is not clear how they determined the mass ratio. The value 0.400 is rather ratio of radii than ratio of masses.
In my analysis of the light curve of IL Mon the data from ASAS-3 were used because these CCD measurements were obtained with standard filter V while ROTSE photometry was done with a CCD camera without filter. Nevertheless, the accuracy of individual measurements from ASAS-3 sky survey is low when compared to targeted photometry with a larger telescope. There is no photometry in two or more filters and no spectroscopic data for IL Mon, except the old determination of spectral type A0 by Götz and Wenzel (1961). Therefore my aim was to obtain only approximate parameters with the use of the computer program Binary Maker 2.0 (Bradstreet, 1993).
From the duration of primary eclipse it follows that the sum of relative radii is equal to 0.40. This value was kept fixed and relative radii of individual components were changed only within it (the step for change of relative radii was 0.01). The effective temperature of the primary component was set to 10000 K which corresponds to the spectral type A0V. The mass ratio, which is unknown at present, was fixed arbitrarily at 1.00. No third light was assumed in this preliminary study.
Fitting synthetic light curves to real data led to a group of equally good solutions within the range 0.10-0.22 and 0.30-0.18 for relative radii of the primary and the secondary component, respectively. It means that real relative radii are somewhere within these values. Five selected complete solutions are presented in Table 2 where individual lines contain the effective wavelength of observational data, relative radii (r1, r2), fractional luminosities (l1, l2), effective temperatures (T1, T2) in Kelvins, limb darkening coefficients (x1, x2), gravity darkening coefficients (g1, g2), reflection coefficients (a1, a2), and inclination of orbital plane (i) in degrees. Parameters with number 1 concern the primary component, those with number 2 relate to the secondary component.
Table 2: Selected light curve solutions for IL Mon.
lambda (nm) 550 550 550 550 550 r1 0.10 0.13 0.16 0.19 0.22 r2 0.30 0.27 0.24 0.21 0.18 l1 0.561 0.724 0.845 0.931 0.978 l2 0.439 0.276 0.155 0.069 0.022 T1(K) 10000 10000 10000 10000 10000 T2(K) 5300 5300 5200 4900 4400 x1 0.48 0.48 0.48 0.48 0.48 x2 0.79 0.79 0.80 0.82 0.84 g1 1.00 1.00 1.00 1.00 1.00 g2 0.32 0.32 0.32 0.32 0.32 a1 1.00 1.00 1.00 1.00 1.00 a2 0.50 0.50 0.50 0.50 0.50 i(°) 77.6 78.3 79.4 81.0 83.6 |
The program Binary Maker 2.0 calculates gravitational and rotational distortions of component stars with the use of the Roche model but in the case of IL Mon the deviations from the spherical model do not exceed a few percent. The uncertainty of the light curve solution is larger then these deviations therefore only average values for the relative radii are given in Table 2. Eclipses are partial in all the solutions but in the first case (r1 = 0.10) only small area near pole of the primary star is visible in phase 0.0. These solutions clearly show that the secondary component cannot be a main sequence star. It must be either a subgiant of spectral type G8IV-K4IV or a giant of spectral type about G3III. The results do not enable to say whether IL Mon is a detached or semi-detached system.
For better understanding this eclipsing binary more precise photometry, at least in two colours, is needed. It is possible that in the middle of primary eclipse there is a phase of constant light lasting less than 1 hour that is not discernible in the ROTSE and ASAS-3 data. Also spectroscopic observations are necessary either for verifying the spectral type of primary component or determination of radial velocity curves or search for possible third component. Determining further times of minimum light would be also desirable.
Acknowledgement. This work made use of the SIMBAD database, operated at CDS, Strasbourg, France, and The Astrophysics Data System of NASA.
References:
Ahnert P., 1976, Mitt. Veränd. Sterne, 7, Nr. 7, 171
Bradstreet D. H., 1993, Binary Maker 2.0: Light Curve Synthesis Program, Contact Software, Norristown, PA
Dvorak S. W., 2004, IBVS, No. 5542
Dworak T. Z., 1975, Acta Astron., 25, 383
Götz W., Wenzel W., 1961, Mitt. Veränd. Sterne, Nr. 570
Herczeg T., Kerrigan J., 1974, Bull. American Astron. Soc., 6, 223
Hübscher J. et al., 2005, BAV Mitt., Nr. 174
Kholopov P. N. et al., 1985-1987, General Catalogue of Variable Stars, 4th edition., Vol. I-III, Moscow
Kreiner J. M., 2004, Acta Astron., 54, 207
Kukarkin B. V. et al., 1958, General Catalogue of Variable Stars, 2nd edition., Moscow
Kukarkin B. V. et al., 1969-1971, General Catalogue of Variable Stars, 3th edition., Vol. I-II, Moscow
Molik P., 2007, Open Europ. J. Var. Stars, No. 60
Pojmanski G., 2003, Acta Astron., 53, 341, The All Sky Automated Survey
Svechnikov M. A., Istomin L. F., Grechova O. A., 1980, Perem. Zvezdy, 21, 413
Svechnikov M. A., Kuznetsova E. F., 1990, Catalogue of Approximate Photometric and Absolute Elements of Eclipsing Variable Stars. Vols 1, 2. Sverdlovsk, Ural University Press
Whitney B. S., 1951, Astron. J., 55, 230
Wozniak P. R. et al., 2004, Astron. J., 127, 2436, Northern Sky Variability Survey
SHON - Contents:
| Go top |